Square Graph
Square Graph
Problem Statement
Takahashi has received an undirected graph with N vertices, numbered 1, 2, ..., N. The edges in this graph are represented by (ui, vi). There are no self-loops and multiple edges in this graph.
Based on this graph, Takahashi is now constructing a new graph with N2 vertices, where each vertex is labeled with a pair of integers (a, b) (1 ≤ a ≤ N, 1 ≤ b ≤ N). The edges in this new graph are generated by the following rule:
- Span an edge between vertices (a, b) and (a', b') if and only if both of the following two edges exist in the original graph: an edge between vertices a and a', and an edge between vertices b and b'.
How many connected components are there in this new graph?
Constraints
- 2 ≤ N ≤ 100,000
- 0 ≤ M ≤ 200,000
- 1 ≤ ui < vi ≤ N
- There exists no pair of distinct integers i and j such that ui = uj and vi = vj.
Input
The input is given from Standard Input in the following format:
N M u1 v1 u2 v2 : uM vM
Output
Print the number of the connected components in the graph constructed by Takahashi.
Sample Input 1
3 1 1 2
Sample Output 1
7
The graph constructed by Takahashi is as follows.
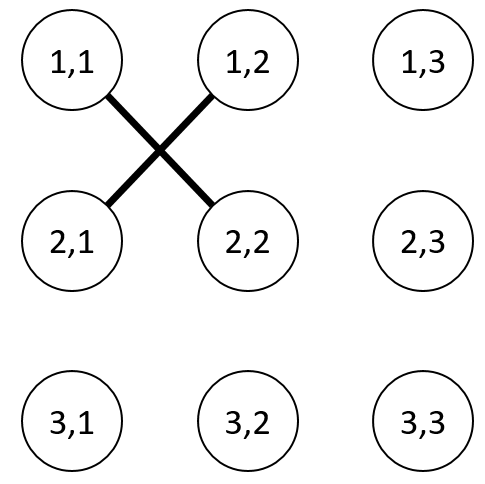
Sample Input 2
7 5 1 2 3 4 3 5 4 5 2 6
Sample Output 2
18
Time Limit: 2 Seconds
Memory Limit: 1024MB
Your best score: 0
Source: AGC 011C
Memory Limit: 1024MB
Your best score: 0
Source: AGC 011C
| Subtask | Score |
|---|---|
| 1 | 100 |
| 2 | 0 |